Basics of Ferrite and Noise Countermeasures

1. What is Ferrite?

Ferrite was invented by Dr. Kato and Dr. Takei in 1930 and is an oxide magnetic material whose main ingredient is iron (Figure 1) Ferrite is classified into soft ferrite (magnetic core material) and hard ferrite (magnet material). TDK was established for producing soft ferrite in 1935.

Figure 1: The First Ferrite Core in the World

Firstly, differences between soft ferrite and hard ferrite will be explained.

Figure 2: B-H Curve of Magnetic Material

Figure 2 shows what is called the B-H curve (magnetic history curve) of magnetic material, showing the flux density B that flows in a magnetic material when a magnetic field H is applied. It is easy to understand if the magnetic material is imagined as an electrical conductive material, the magnetic field as an electric field, and the flux density as an electric current. When a voltage is applied to the common electrical conductive material, a current flows in proportion to the voltage; then, if the voltage is decreased, the current decreases in proportion to the voltage (Ohm’s Law). In the case of the magnetic material, the flux density non-linearly increases against the magnetic field. If the magnetic field is decreased after being increased, the flux density decreases while drawing a different curve from that obtained when the magnetic field is increasing. Therefore, the curve is called a history curve (hysteresis curve). In the case of hard ferrite, when the magnetic field first increases the flux density does not change so much, however, when the magnetic field becomes extremely strong, a sudden flux density flows to create a magnet. Under such circumstances, a magnetic field in the reverse direction would not restore the original conditions. Such a property is called magnetically hard. The stronger the magnetically hard property, the more stable the magnet, as it would not be easily restored by an external magnetic field and would thus make an excellent magnetic material.On the other hand, with soft ferrite, when the magnetic field is increased, the flux density immediately starts to flow and magnetization occurs. However, when trying to restore conditions by applying a magnetic field in the opposite direction, the original conditions will be easily restored. Such a property is called magnetically soft. When used as a transformer or a coil, the stronger the magnetically soft nature, the higher the performance, as the magnetic core with even a small change in the magnetic field experiences a large change in the flux density, again making an excellent magnetic material.

2 B-H Curve of Soft Ferrite

Let’s enlarge the B-H curve of soft ferrite again (Figure 3). Just after the ferrite is produced, no external magnetic field is applied to the ferrite, and it is under a state with no magnetization (origin O). As the external magnetic field H is increased, the flux density B flows (magnetized) by the magnetic field in the ferrite along a curve called an initial magnetization curve. When H is increased up to a point where B no longer increases (not correct, strictly speaking), the maximum B is called a saturation flux density B_s, denoting a maximum flux density for the magnetic material flow. Now, H is decreased from the state of B_s. As explained before, B decreases while drawing a different curve from the initial magnetization curve. B does not return to the original condition even when H becomes zero and magnetism remains in the ferrite. The value of B then is called residual magnetization B_r. H then begins to be applied in the reverse direction from the state of B_r. When B is restored to the state of zero, H is called a coercive force H_c. As H is continued to be applied, this time B reaches Bs in the opposite direction, and later as H is reduced, B_r appears in the opposite direction. When H is applied in the initial direction, B reaches B_s after H passes Hc.

Figure 3: B-H Curve of Soft Ferrite

When using soft ferrite as a magnetic core, since in most cases it will be used with an alternative current, the core may generally be considered at the origin of the B-H curve. When applying an alternating magnetic field to the core, the alternating B-H loop becomes large along the initial magnetization curve. Next, descriptions will be given for permeability μ using the initial magnetization curve.

3 Initial Magnetization Curve and Permeability

When using the ferrite for noise countermeasures, permeability μ will be very important characteristics. The relation among permeability μ, magnetic field H, and saturation flux density B is represented by the following formula.

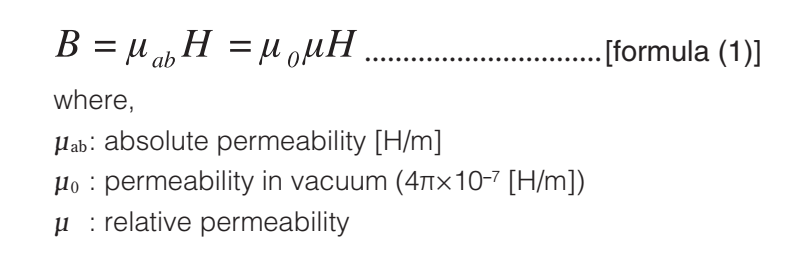
As shown by formula (1), μ is a gradient of the B-H curve. In the world of physics, μ is usually represented by absolute permeability. However, it is practically convenient to be represented by relative permeability. Therefore, when talking of μ, the value represents the relative permeability in general. Relative permeability denotes how many times the magnetic material allows magnetic flux to pass more easily than a vacuum (the air).

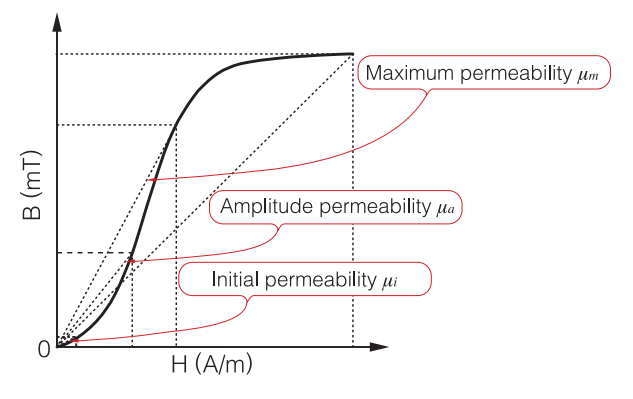
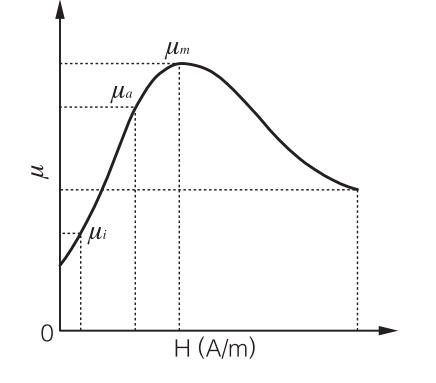
Let’s consider using the initial magnetization curve of Figure 4. The permeability at the start part (very close to an origin O) of the initial magnetization curve is called initial permeability μ_i. In many cases, permeability denotes this value. The value on a catalog of ferrite materials denotes initial permeability.

Figure 4: Initial Magnetization Curve and Permeability of Soft Ferrite

As magnetic field intensity H is increased from an initial permeability area, flux density B increases along the initial magnetization curve. When fully driving a magnetic core by an alternating current (uniformly between a plus side and the minus side across the origin O), the permeability has a gradient connecting the point on the initial magnetization curve with the origin O. Such permeability is called amplitude permeability μa. The initial permeability mentioned above can be described as amplitude permeability at the time of significantly small amplitude.

Amplitude permeability μ_a generally increases as H increases, and after reaching a local maximum (maximum permeability μ_m) to decrease again. Therefore, it is necessary to recognize that the permeability of ferrite materials is not constant μ_i, but changes according to the magnitude of the excitation.

4 Temperature Change of Permeability μ and Curie Temperature

The permeability of ferrite changes according to temperature. The permeability of ferrite usually increases as temperature rises. After reaching a local maximum at a certain temperature, the permeability of magnetic materials disappears (comes to be equal to the permeability of the air, μ =1) as the temperature rises further. The temperature at which the magnetic property disappears from magnetic materials is called the Curie temperature. The Curie temperature of ferrite is usually obtained from the temperature when μi becomes 1 on a line, which is obtained by connecting a point where the temperature characteristics of μi drops from a local maximum μ_i_max to a point of 80 % of μ_imax with a point of 20 % of μ_imax (refer to Figure 5).

Figure 5: Temperature Change of Permeability and Curie Temperature

The temperature change of permeability depends on the kind of ferrite. To use ferrite over a wide temperature range, stable characteristics can be obtained by selecting a ferrite with little change in permeability by temperature. As an index of temperature change of permeability, temperature coefficient αμand relative temperature coefficient αF of permeability are cited, being described as such in the catalog.

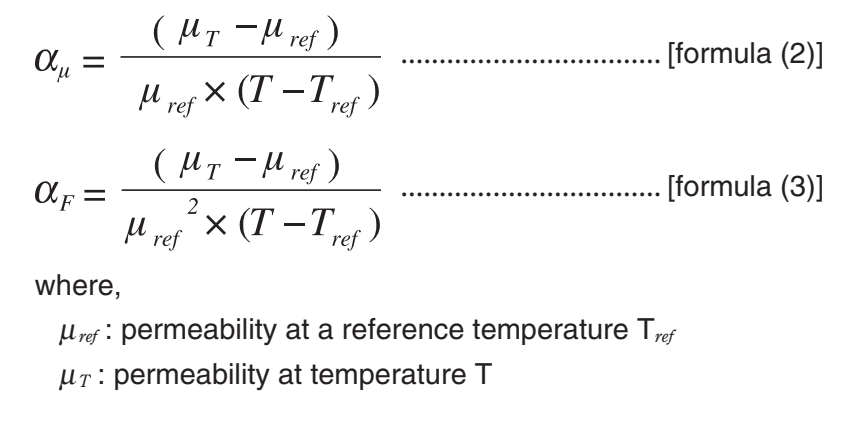
As the reference temperature T_ref=25°C is recommended. The temperature T is decided by a temperature zone where the core is used, being selected from –40°C, –25°C, + 5°C, + 55°C, + 85°C in general.

5 Core Constant

Descriptions will be given to the relation between permeability, and inductance and impedance, however, knowledge about the core constant is needed beforehand.
When calculating electric circuit values (L, R, Z, i, v) from magnetic materials values (μ, B, H), a cross-section area A (the area where the magnetic flux passes) and a magnetic path length l (the distance in which the flux flows) of the core need to be calculated. As for the core in actual use, it is necessary to obtain an effective cross-sectional area A_e, and an effective magnetic path length l_e in consideration of such a factor as the difference in cross-sectional area for each part of the core. In the catalog of ferrite cores, these A_e and l_e are described. These values are available and they can be calculated as follows:

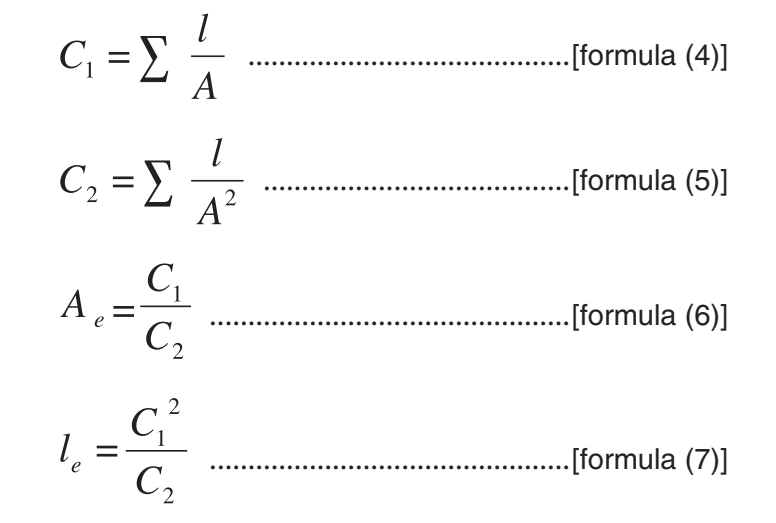
where, C₁, C₂: core constant.

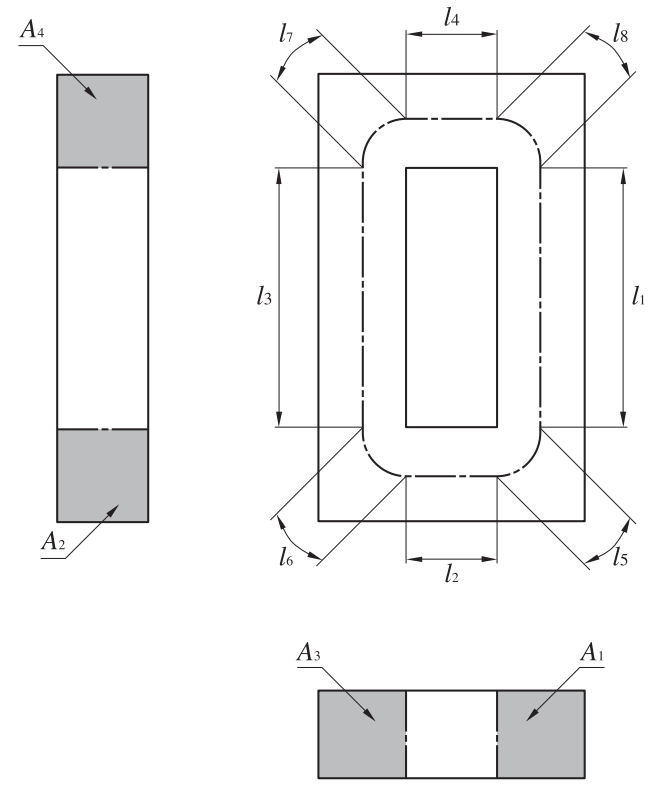
Even for a core with a complicated shape we can calculate an effective cross-sectional area Ae and an effective magnetic path length le of the entire core in consideration of dividingeach part of the core to totalize the cross-sectional area A and magnetic path length l by formulas (4) and (5). In the case of a ring-shaped core, Ae and le can be calculated by the following formulas.

Figure 6: Dimensional Drawing of a Ring Core

In the case of a rectangular (picture frame shape) core, the next formula can be used.

Figure 7: Dimensional Drawing of Rectangular (Picture Frame Shape) Core

6 Permeability and Inductance

A relation between permeability and inductance is given by the following formula.

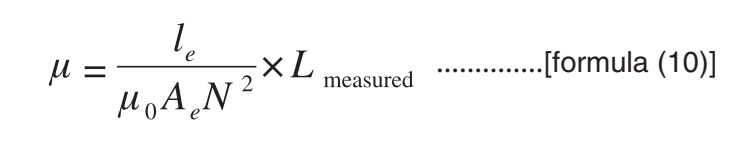
where,
A_e : effective cross-sectional area (m_²)
l_e : effective magnetic path length (m)
μ₀ : permeability in vacuum = 4π×10^–7(H/m)
N : Number of turns of measurement coil
L_measured : measurement inductance (H)

The magnetic field intensity H applied to the core (or flux density B) can be decided by the current flowing through the measurement coil (or the voltage across the coil). A relation between the current i flowing through the coil and the magnetic field intensity H is given by the following formula.

where,
l_e : effective magnetic path length (m)
N : Number of turns of measurement coil
i : electric current flowing through measurement coil (A)

Beware that H is in proportion to i. When applying an alternating magnetic field to a core, the magnetic field intensity to be applied is usually represented by a zero-to-peak value. Accordingly, the current also has to use I₀_–P value. For example, current values displayed in such devices as an LCR meter are an effective value, therefore, in order to obtain I_0–P, it is necessary to multiply by √2 (when the applied alternating magnetic field is a sinusoidal wave). A relation between the voltage e across a coil and the flux density B is given by the formula as follows.

where,
A_e : effective cross-sectional area (m²)
N : Number of turns of measurement coil
е: voltage across a measurement coil (V)

When an alternating magnetic flux flows in the core, magnetic flux B is usually represented by a zero-peak value as well as the magnetic field intensity H. In this case, however, since flux density is an integral of voltage, it is necessary to calculate an integral value of voltage. When the voltage is sinusoidal, the following formula can be used for calculation.

where,
A_e : effective cross-sectional area (m²)
N : Number of turns of measurement coilf
f: frequency (Hz)
V_rms: effective voltage across measurement coil (V)

Initial permeability μi is permeability of a minute excitation level. At which level the measurement is performed is specified in the standard (IEC 60401-3 and JIS-C-2560-1)(B<0.5 mT). In the measurement, output of the LCR meter is adjusted so as to be a specified excitation level.

7 Complex Permeability and Impedance

Winding and excitation by the alternative current cause core loss in actual magnetic materials. In terms of an electric circuit, L-element is connected with R-element in series, the impedance being represented by R + jωL. This relation will be applied to permeability and such complex permeability is considered as follows.

In this formula, μ ́ is a real part, denoting an inductance component, and μ ̋ is an imaginary part, denoting a resistance component, respectively. μ ́ is the same as permeability explained in the section 6 “Permeability and Inductance”.|∙μ|, μ ́, and μ ̋ can be obtained by formulas as follows.

Then, tangent tanδ of a loss angle is represented by formula (18), therefore, a relation of formula (19) exists between the real and the imaginary parts of the complex permeability and tanδ.

This tanδ is called a loss factor, representing a loss of magnetic materials. A relative loss factor tanδ/μ_i is obtained by dividing tanδ by μ_i, being used as an index representing the loss of magnetic materials, as well.

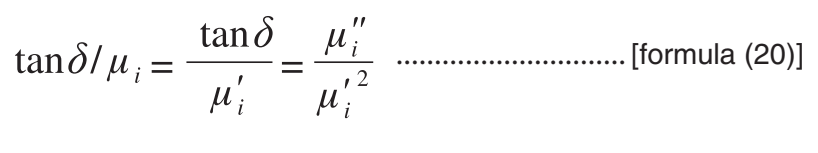
8 Frequency Characteristics of Permeability and Snoek’s Limit

The permeability of ferrite remains constant up to a certain frequency. When the frequency becomes high, however, B can not follow the change in H, causing a phase lag. Because of this, L-component (μ ́) begins to decrease and R-component (μ ̋ ) begins to increase.Then, ferrite exhibits a phenomenon that the higher the permeability of the material, the earlier μ ́ drops. This is called Snoek’s limit. It is desirable that ferrite material having high permeability be used for a high frequency. However, because of the Snoek’s limit, ferrite materials have to be selectively used according to the frequency range in use. Figure 8 shows frequency characteristics of initial permeability of ferrite materials having different initial permeability and Snoek’s limit line. In consideration of noise removal, however, this phenomenon is not always wrong, which will be described later.

Figure 8: Frequency Characteristics of Ferrite μiand Snoek’s Limit

9 Kinds of Ferrite

The chemical formula of ferrite is MO∙Fe₂O₃, where M denotes a divalent metal ion. Metal ions such as Fe, Mn, Zn, Ni, Mg, Co, and Cu can be substituted for M and ferrite materials having a variety of characteristics are obtained based on the kinds and ratios of the metal ions. Mn-Zn ferrite and Ni-Zn ferrite are typical ferrite materials.Mn-Zn ferrite has excellent magneto-electrical characteristics because μi and Bs are high and the core loss is low. On the other hand, since low specific resistance (volume resistance) is a weak point, direct winding to the core is not possible but an insulative bobbin or case has to be interposed, resulting in a large shape. Because of high permeability, usable frequency is limited about 1 MHz or less due to Snoek’s limit, therefore, as a noise countermeasure

Mn-Zn ferrite is used for a common mode line filter choke of a power source line.

Compared with Mn-Zn ferrite, Ni-Zn ferrite has low μi and Bs, having a large core loss, however, specific resistance is high and almost regarded as an insulator. Accordingly, direct winding on the core is possible and no bobbin is required. Ni-Zn ferrite is used for small coils and chip inductors, and for noise countermeasures being frequently used for bead core and clamp filters (refer to Figure 9).

10 Characteristics of Ferrite Material for Noise Countermeasures

Tables 1 and 2 show a characteristic table of noise-countermeasure ferrite material by TDK. Ferrite materials of Table 1 are mainly Ni-Zn series, being used for round-type cables (including bead core), flat cables, and connectors (refer to Figure 10). Ferrite materials of Table 2 are mainly Mn-Zn series, being used for common mode chokes (refer to Figure 11).

Figure 9: Characteristics of Mn-Zn and Ni-Zn Ferrite

Figure 10: Core Shape for Round-type and Flat Cables, and Connector

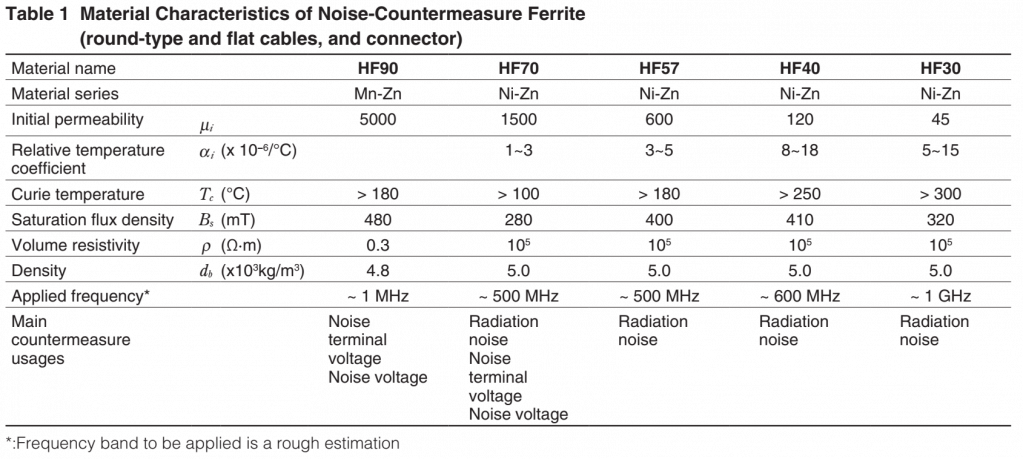
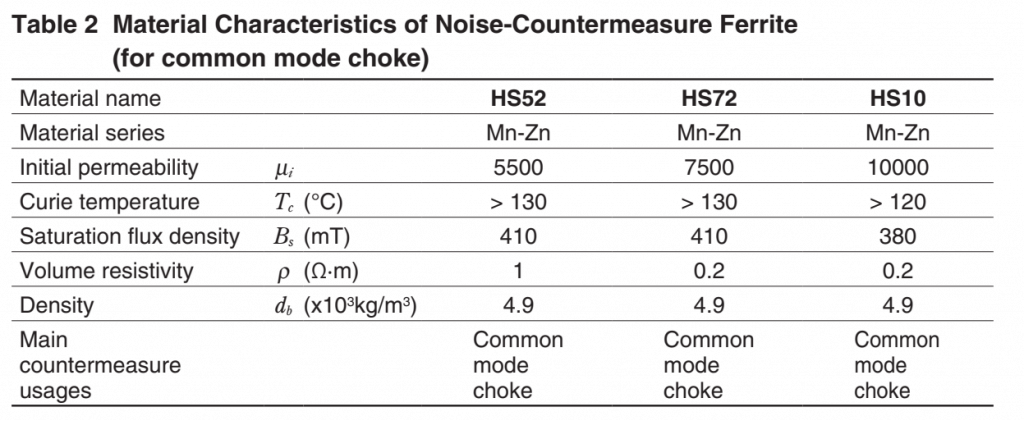
Figure 11: Common Mode Choke Core Configuration

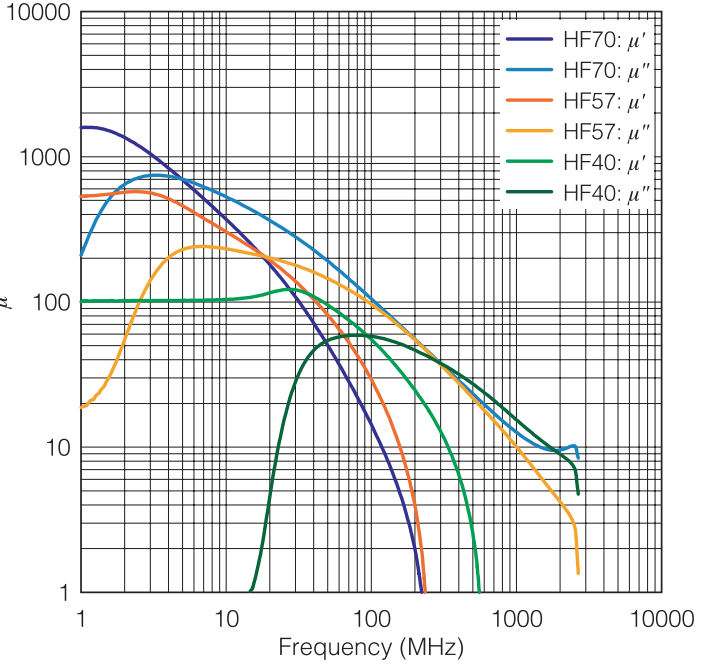
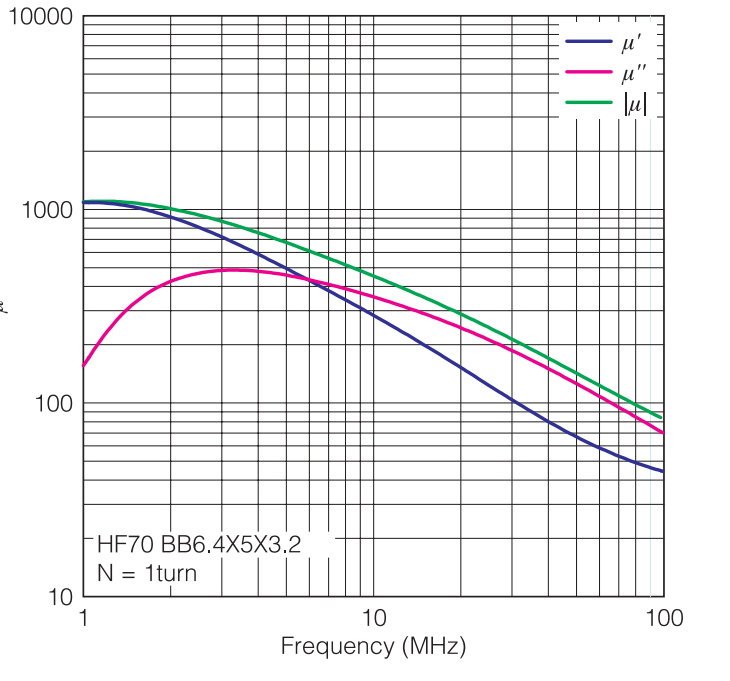
Figure 12 shows frequency characteristics of μ ́ and μ ̋ of materials cited in Table 1.Pay attention that μ ̋ attains a peak value near the frequency at which μ ́ begins to fall for all characteristics.

Figure 12-1: Frequency Characteristics of μ HF90 Materials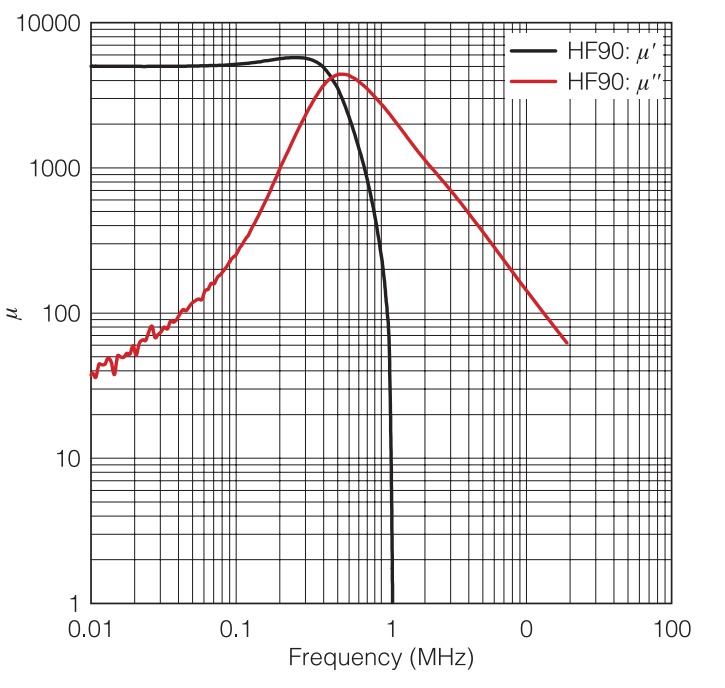

Figure 12-2: Frequency Characteristics of μ HF40, 57, 70 Materials

11 Principle of Noise Countermeasures by Ferrite

Ferrite cores are used for a variety of noise countermeasures, being largely classified into such categories as:

inductance element for configuring a filter,
to cut off noises by impedance,
to absorb noises (transform into heat) by R-component, and4. shielding.

When using the ferrite core as the inductance element, it is used as an L-component. Therefore, it is important to use the ferrite material in a frequency band where μ ́ does not decrease.Noise countermeasure ferrite cores are most commonly used to cut off noises by impedance. In this case, to select a ferrite material, a core configuration, and the number of turns is important, so as to acquire impedance large enough to obtain a sufficient noise prevention effect in the frequency band of noises to be prevented.

Frequency characteristics of impedance by each material and shape are described for your reference in the catalog. The catalog is downloadable from the URL as follows: http://www.tdk.co.jp/tefe02/emc.htm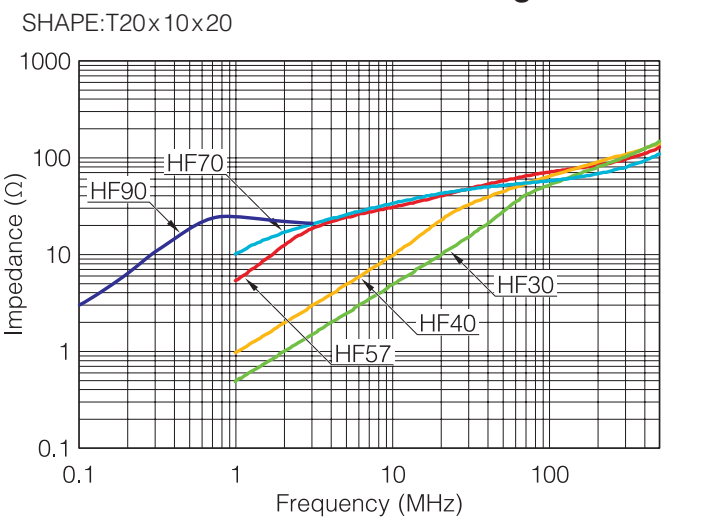

Figure 13: Frequency Characteristics of Impedance Described in the Catalog

Noises are blocked by impedance, however, it should be noted that since reflection occurs at the edge of the impedance element, noises will not disappear.

A usage to absorb noises by R-component is similar to the usage to block noises by the above-mentioned impedance. The difference is that a μ ̋ component is positively used instead of a μ ́ component. As explained before, since μ" is an R-component, when using ferrite in a frequency band where μ" is high, noises can be transformed into heat by R to be absorbed without reflecting noises.

A small ring core called a bead core is a typical product for this type of usage. Ferrite for a radio wave absorber also utilizes this principle. Figure 14-1 shows frequency characteristics of R, X, and |Z| of the beads core. While in the low frequency region, reactance X is dominant and noises are reflected, when the frequency gets higher, X intersects R at a certain frequency. After the reversal, R becomes dominant. In order to absorb noises, it is necessary to select the frequency band where R becomes dominant. The frequency at which X and R intersect depends on the ferrite materials.

Figure 14-1: Frequency Characteristics of Beads Core

Figure 14-2 shows frequency characteristics of μ ́, μ ̋ , and |μ| calculated from impedance characteristics of the bead core. The above mentioned formulas (15), (16), and (17) are used. It will be understood from these formulas and the graph that there are relations between μ ́ and L(X), μ ̋ and R, and |μ| and | Z |, respectively.

Figure 14-2: Frequency Characteristics of μ Beads Core

Accordingly, in order to select a ferrite material suitable for the frequency band to absorb noises, the material may be selected so that μ ̋ becomes high at the frequency to absorb noises in the graph of Figure 12.

Using ferrite as a shield takes advantage of a principle that fluxes flowing in the space are guided into the ferrite because of the high permeability of the ferrite. As explained in the above, permeability expresses how easily fluxes flow compared with the air. Some ferrite material exhibits high permeability, from as high as several thousands to several tens of thousands, making them suitable for use as a shield.

In that case, μ ́ becomes important. It is necessary to select a material having μ ́ as high as possible at the frequency of the noise to be shielded.

Beware that when shielding using ferrite, the flux by the noise only changes paths dependent on the ferrite but does not disappear. Therefore, when a component easily subjected to noises is located near a noise source, a ferrite plate is attached to the side of the component to avoid the concentration of noises.

Although not really needed, descriptions will be given for a method of shielding without using ferrite. It is shielding by conductors in the form of a metal shielding case. The metal must not be composed of magnetic materials.

When an alternating magnetic flux intersects with a metal, an eddy current flows in the metal and generates a magnetic flux in the direction needed to cancel the alternating magnetic flux. Because of the magnetic flux, the alternating flux is cancelled and disappears. Accordingly, in order to prevent flux caused by noises from going outside, it is effective to attach a metal plate near the noise source or to surround it by a metal case.

However, the eddy current is generated at a relatively higher frequency and the generated frequency depends on the conductivity and thickness of the conductor, therefore, it is necessary to know them in advance. In some cases, no eddy current is generated by a magnetic flux of low frequency. In such a case, a further effect may be obtained in combination with shielding by permeability.